본 포스팅에서는 확률변수 $X$의 분포가 알려져 있을 때 확률변수 $Y=u(X)$의 분포를 구하는 방법에 대해 다룬다.
이산형 확률변수의 경우
1. 공정한 동전을 2회 던졌을 때 앞면이 나오는 횟수를 $X$라 하자. $X$의 확률밀도함수는 다음과 같다. $$f_X(x) = \begin{cases} \cfrac{1}{4}, & x = 0,2 \\ \cfrac{1}{2}, & x = 1 \end{cases}$$ 이로부터 $Y = (X-1)^2$의 확률밀도함수를 구해 보자. $Y$가 취할 수 있는 값은 $0$ 또는 $1$이고, 이에 대응하는 확률은 각각 $$\begin{align} P(Y=0) &= P(X=1) = \frac{1}{2} \\ P(Y=1) &= P(X=0) + P(X=2) = \frac{1}{2} \end{align}$$이다. 즉, $$f_Y(y) = \frac{1}{2},\ \ y \in \{0,1\}$$임을 알 수 있다. 일반적으로 이산형 확률변수 $X$의 확률밀도함수가 $f_X(x)$로 주어졌을 때, $Y=u(X)$의 확률밀도함수 $f_Y(y)$는 다음과 같다. $$ f_Y(y) = \sum_{x:\ u(x)=y}f_X(x)$$
2. 확률변수 $X_1$, $X_2$가 서로 독립이고 각각 $\text{B}(n_1, p)$, $\text{B}(n_2, p)$를 따를 때, $Y=X_1+X_2$의 확률밀도함수를 구해 보자. $$\begin{align} f_Y(y) &= P(Y=y) \\ &= \sum_{i=0}^{y} P(X_1 = i,\ X_2 = y-i) \\ &= \sum_{i=0}^{y} P(X_1 = i) P(X_2 = y-i) \\ &=\sum_{i=0}^{y} \binom{n_1}{i} \binom{n_2}{y-i} p^{y}(1-p)^{n_1+n_2-y} \\ &= \binom{n_1+n_2}{y} p^{y}(1-p)^{n_1+n_2-y}\end{align}$$ 이로부터 $Y \sim \text{B}(n_1+n_2, p)$임을 알 수 있다. 위의 마지막 등식에서는 방데르몽드 항등식(Vandermonde's identity)이 사용되었다.
3. 확률변수 $X_1$, $X_2$가 서로 독립이고 각각 $\text{Pois}(\lambda_1)$, $\text{Pois}(\lambda_2)$를 따를 때, $Y = X_1 + X_2$의 확률밀도함수를 구해 보자. $$\begin{align} f_Y(y) &= \sum_{i=0}^{y} P(X_1 = i) P(X_2 = y-i) \\ &=\sum_{i=0}^{y} \frac{{\lambda_1}^i {\lambda_2}^{y-i} e^{-(\lambda_1+\lambda_2)}}{i ! (y-i) !} \\ &=\sum_{i=0}^{y} \binom{y}{i} {\lambda_1}^i {\lambda_2}^{y-i} \frac{e^{-(\lambda_1 + \lambda_2)}}{y!} \\ &=\frac{(\lambda_1 + \lambda_2)^{y} e^{-(\lambda_1 + \lambda_2)}}{y!} \end{align}$$ 이로부터 $Y \sim \text{Pois}(\lambda_1 + \lambda_2)$임을 알 수 있다. 위의 마지막 등식에서는 이항정리가 사용되었다.
연속형 확률변수의 경우
1. 확률변수 $X$의 확률밀도함수가 $f_X(x)$일 때 $Y = aX+b$의 확률밀도함수를 구해 보자. 이 경우 먼저 $Y$의 누적분포함수를 구한 후 미분을 통해 확률밀도함수를 얻을 수 있다. $a$가 양수인 경우 $$\begin{align} F_Y(y) &= P(Y \le y ) \\ &= P(aX+b \le y) \\ &= P\! \left (\! X \le \frac{y-b}{a} \!\right ) \\ &= F_X\! \left (\! \frac{y-b}{a}\! \right ) \end{align}$$이고, 따라서 $$\begin{align} f_Y(y) &= \frac{dF_Y(y)}{dy} \\ &= \frac{d}{dy}F_X\! \left ( \! \frac{y-b}{a} \! \right) \\ &=\frac{1}{a} f_X \! \left( \! \frac{y-b}{a} \! \right)\end{align}$$이다. 유사한 전개를 통해 $a$가 음수인 경우 $ f_Y(y) = -\frac{1}{a} f_X \! \left ( \! \frac{y-b}{a} \! \right)$임을 알고, 이를 종합하여 $$f_Y(y) = \frac{1}{\vert a \vert} f_X \! \left ( \! \frac{y-b}{a} \! \right) $$로 표현할 수 있다.
2. 확률변수 $X$의 확률밀도함수가 $f_X(x)$일 때 $Y = X^2$의 확률밀도함수를 구해 보자. 역시 $Y$의 누적분포함수로부터 시작하면 $$\begin{align} F_Y(y) &= P(Y \le y) \\ &=P(X^2 \le y) \\ &= P(-\sqrt{y} \le X \le \sqrt{y}) \\ &= P(X \le \sqrt{y}) - P(X \le -\sqrt{y}) \\ &=F_X(\sqrt{y}) - F_X(-\sqrt{y}) \end{align}$$이고, 따라서 $$\begin{align} f_Y(y) &= \frac{dF_Y(y)}{dy} \\ &= \frac{d}{dy} [F_X(\sqrt{y})-F_X(-\sqrt{y})] \\ &= \frac{1}{2\sqrt{y}} [f_X(\sqrt{y}) + f_X(-\sqrt{y})] \end{align}$$이다.
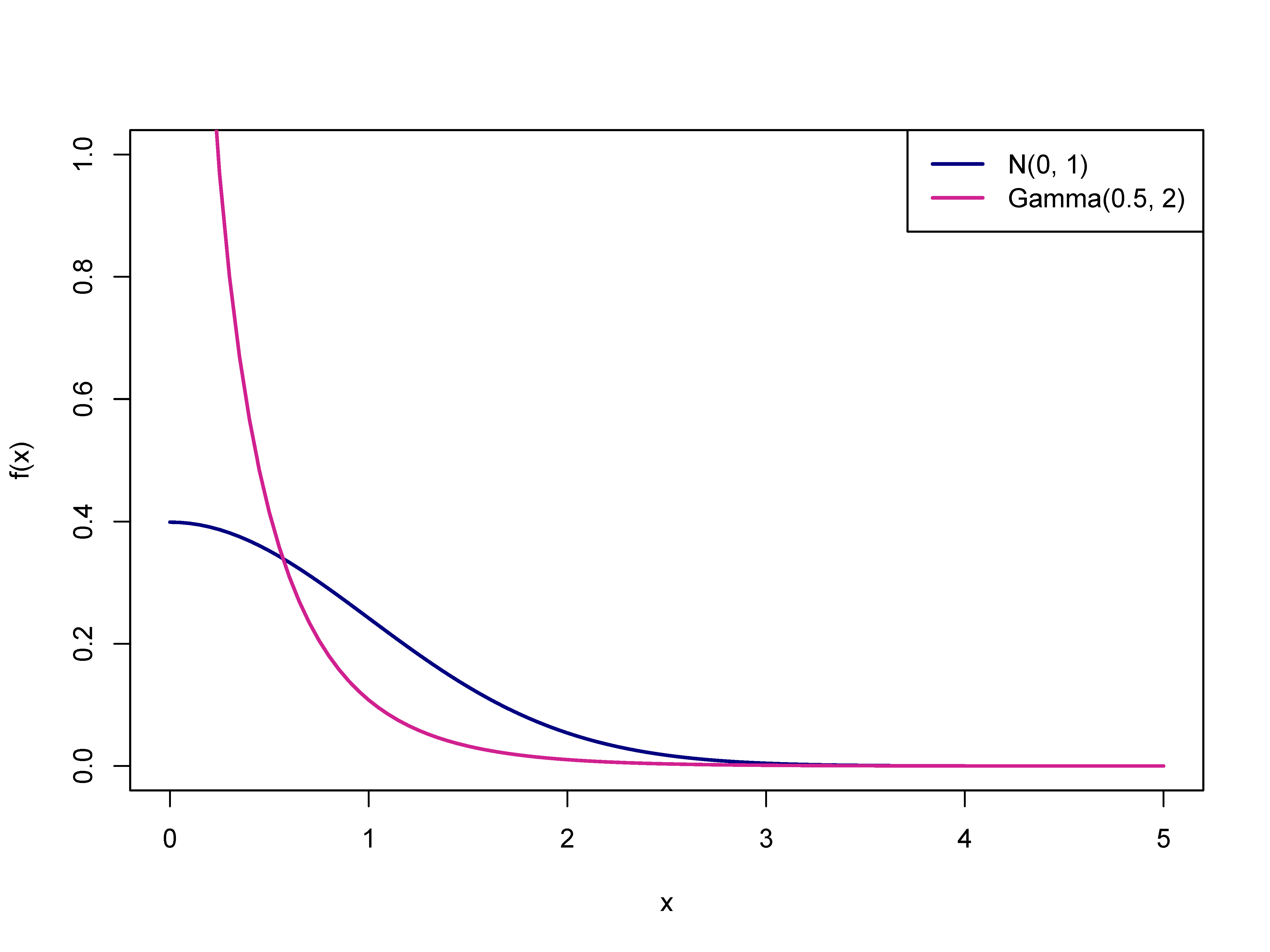
2-1. $X \sim \text{N}(0, 1)$인 경우를 생각해 보자. 표준정규분포곡선은 $y$축을 중심으로 좌우 대칭이므로 $\phi(-x) = \phi(x)$이고, 따라서 $$\begin{align} f_Y(y) &=\frac{1}{\sqrt{y}}\phi(\sqrt{y}) \\ &=\frac{1}{\sqrt{2 \pi}}y^{-\frac{1}{2}}e^{-\frac{y}{2}},\ \ y \in (0, \infty) \end{align}$$이다. 즉, $Y \sim \text{Gamma}(\frac{1}{2}, 2)$임을 알 수 있다.
3. 일반적으로 연속형 확률변수 $X$의 확률밀도함수가 $f_X(x)$이고 $y=u(x)$가 일대일 함수일 때, $Y = u(X)$의 확률밀도함수는 다음과 같이 나타낼 수 있다. $$f_Y(y) = f_X[u^{-1}(y)] \left\vert \frac{du^{-1}(y)}{dy} \right\vert $$ 이는 1에서처럼 누적분포함수를 이용해 보일 수도 있지만, 다음과 같이 치환적분을 이용할 수도 있다. 편의상 $y=u(x)$가 단조증가인 경우만을 고려하자. 확률밀도함수의 정의에 따르면 구간 $[a, b]$에 대하여 $$P(a \le Y \le b) = \int_{a}^{b} f_Y(y)\ dy $$이다. 그런데 $$\begin{align} P(a \le Y \le b) &= P(a \le u(X) \le b) \\ &= P[u^{-1}(a) \le X \le u^{-1}(b)] \\ &= \int_{u^{-1}(a)}^{u^{-1}(b)} f_X(x)\ dx \end{align}$$이고, 이 때 $x = u^{-1}(y)$로 치환하면 $$P(a\le Y \le b) = \int_{a}^{b} f_X[u^{-1}(y)] \frac{du^{-1}(y)}{dy}\ dy$$이 되어 원하는 결과를 얻는다.
4. 확률변수 $X_1$, $X_2$의 결합확률밀도함수가 $f_{X_1, X_2}(x_1, x_2)$일 때 $Y_1=u_1(X_1, X_2)$의 확률밀도함수를 구해 보자. 이 경우 dummy 변수인 $Y_2$를 만들고 치환적분을 통해 $f_{Y_1, Y_2} (y_1, y_2)$를 계산하면 편리하다. $Y_2 = u_2(X_1, X_2)$라 두면 다음과 같이 변환 $\mathbf{u}$를 정의할 수 있다. $$\begin{align} \mathbf{u}(x_1,x_2) &= (u_1(x_1, x_2),\ u_2(x_1, x_2)) \\ &=(y_1, y_2) \end{align}$$ 한편 영역 $A $에 대하여 $$ P[(Y_1, Y_2) \in A] = \iint_{A} f_{Y_1, Y_2}(y_1, y_2)\ dy_1 dy_2$$이다. 그런데 $\mathbf{u}$가 가역일 경우 $$\begin{align} P[(Y_1, Y_2) \in A] &= P[\mathbf{u}(X_1, X_2) \in A] \\ &= P[(X_1, X_2) \in \mathbf{u}^{-1}(A)] \\ &= \iint_{\mathbf{u}^{-1}(A)} f_{X_1, X_2}(x_1, x_2)\ dx_1 dx_2\end{align}$$이고, 이 때 $(x_1, x_2) = \mathbf{u}^{-1}(y_1, y_2)$로 치환하면 $$ \begin{align} &P[(Y_1, Y_2) \in A] \\ = &\iint_{A} f_{X_1, X_2}[\mathbf{u}^{-1}(y_1, y_2)] \vert \det \mathbf{J}_{\mathbf{u}^{-1}}\vert\ dy_1 dy_2 \end{align}$$이다. 이로부터 얻어지는 아래의 식은 3의 결과를 다차원 확률변수로 확장한 것이다. $$ f_{\mathbf{Y}}(\mathbf{y}) = f_{\mathbf{X}}[\mathbf{u}^{-1}(\mathbf{y})] \vert \det \mathbf{J}_{\mathbf{u}^{-1}} \vert $$
5. 확률변수 $X_1$, $X_2$가 서로 독립이고 각각 $\text{Gamma}(\alpha_1, \beta)$, $\text{Gamma}(\alpha_2, \beta)$를 따를 때, $Y_1 = \frac{X_1}{X_1 + X_2}$의 확률밀도함수를 구해 보자. $Y_2 = X_1 + X_2$로 두고 식을 정리하면 $X_1 = Y_1 Y_2$, $X_2 = (1-Y_1)Y_2$이고, $$ \mathbf{J}_{\mathbf{u}^{-1}} = \begin{pmatrix} \cfrac{\partial x_1}{\partial y_1} & \cfrac{\partial x_1}{\partial y_2} \\ \cfrac{\partial x_2}{\partial y_1} & \cfrac{\partial x_2}{\partial y_2} \end{pmatrix} = \begin{pmatrix} y_2 & y_1 \\ -y_2 & 1-y_1 \end{pmatrix}$$이다. 한편 $x_1>0$, $x_2>0$으로부터 $0<y_1<1$, $y_2>0$이고, 따라서 $\vert \det \mathbf{J}_{\mathbf{u}^{-1}} \vert = y_2$이다. 이제 $X_1$, $X_2$의 결합확률밀도함수가 $$f_{X_1, X_2}(x_1, x_2) = \frac{{x_1}^{\alpha_1 - 1} {x_2}^{\alpha_2 -1} e^{-\frac{x_1 + x_2}{\beta}}}{\Gamma(\alpha_1) \Gamma(\alpha_2) \beta^{\alpha_1 + \alpha_2}} $$이므로, $Y_1$, $Y_2$의 결합확률밀도함수는 $$\begin{align} f_{Y_1, Y_2}(y_1, y_2) &= \frac{(y_1 y_2)^{\alpha_1 - 1} [(1-y_1)y_2]^{\alpha_2-1} e^{-\frac{y_2}{\beta}}y_2}{\Gamma(\alpha_1) \Gamma(\alpha_2) \beta^{\alpha_1+\alpha_2}} \\ &= \frac{{y_1}^{\alpha_1 -1} (1-y_1)^{\alpha_2-1} {y_2}^{\alpha_1 + \alpha_2 - 1} e^{-\frac{y_2}{\beta}}}{\Gamma(\alpha_1) \Gamma(\alpha_2) \beta^{\alpha_1 + \alpha_2}} \end{align}$$이다. 그런데 이는 $Y_1$, $Y_2$의 주변확률밀도함수의 곱으로 표현할 수 있다. $$\begin{align} f_{Y_1}(y_1)&= \frac{\Gamma(\alpha_1 + \alpha_2)}{\Gamma(\alpha_1) \Gamma(\alpha_2)} {y_1}^{\alpha_1-1} (1-y_1)^{\alpha_2-1} \\ f_{Y_2}(y_2)&= \frac{1}{\Gamma(\alpha_1 + \alpha_2)\beta^{\alpha_1+\alpha_2}} {y_2}^{\alpha_1 + \alpha_2 -1}e^{-\frac{y_2}{\beta}} \end{align}$$ 이로부터 $Y_1$과 $Y_2$는 서로 독립이고 $Y_2$는 $ \text{Gamma}(\alpha_1 + \alpha_2, \beta)$를 따름을 알 수 있다.
5-1. 위에서 구한 $Y_1$의 분포를 모수가 $\alpha_1$, $\alpha_2$인 베타분포라 하며 $\text{Beta}(\alpha_1, \alpha_2)$로 표기한다. $Y_1$의 기댓값과 분산은 다음과 같다. $$\begin{align} \mathbb{E}(Y_1) &= \frac{\alpha_1}{\alpha_1 + \alpha_2} \\ \text{Var}(Y_1) &= \frac{\alpha_1 \alpha_2}{(\alpha_1 + \alpha_2)^2(\alpha_1 + \alpha_2 + 1)} \end{align}$$ 베타확률변수는 모수의 값에 따라 구간 $(0, 1)$ 상에서 여러 가지 형태의 분포를 가지며, 적절한 변환을 이용하면 임의의 유한 구간 내의 값을 갖는 변수에 대한 확률모형으로 활용될 수 있다.

6. 확률변수 $X_1$, $X_2$가 서로 독립이고 $\text{N}(0, 1)$을 따를 때, $Y_1 = \frac{X_1}{X_2}$의 확률밀도함수를 구해 보자. $Y_2 = X_2$로 놓고 식을 정리하면 $X_1 = Y_1 Y_2$, $X_2 = Y_2$이고, $$ \mathbf{J}_{\mathbf{u}^{-1}} = \begin{pmatrix} \cfrac{\partial x_1}{\partial y_1} & \cfrac{\partial x_1}{\partial y_2} \\ \cfrac{\partial x_2}{\partial y_1} & \cfrac{\partial x_2}{\partial y_2} \end{pmatrix} = \begin{pmatrix} y_2 & y_1 \\ 0 & 1 \end{pmatrix}$$이므로 $\vert \det \mathbf{J}_{\mathbf{u}^{-1}} \vert = \vert y_2 \vert$이다. 이제 $X_1$, $X_2$의 결합확률밀도함수가 $$f_{X_1, X_2}(x_1, x_2) = \frac{1}{2 \pi} e^{-\frac{{x_1}^2 + {x_2}^2}{2}} $$이므로, $Y_1$, $Y_2$의 결합확률밀도함수는 $$\begin{align} f_{Y_1, Y_2}(y_1, y_2) &= \frac{1}{2 \pi} e^{-\frac{{y_2}^2 ({y_1}^2 +1)}{2}} \vert y_2 \vert \end{align} $$이고, $f_{Y_1, Y_2}(y_1, -y_2) = f_{Y_1, Y_2}(y_1, y_2)$임을 이용하면 $$\begin{align} f_{Y_1}(y_1) &= \int_{-\infty}^{\infty} f_{Y_1, Y_2}(y_1, y_2)\ dy_2 \\ &= 2 \int_{0}^{\infty} f_{Y_1, Y_2} (y_1, y_2)\ dy_2 \\ &= \frac{1}{\pi} \int_{0}^{\infty} y_2 e^{-\frac{{y_2}^2 ({y_1}^2 + 1)}{2}} \ dy_2 \\ &=\frac{1}{\pi ({y_1}^2 + 1)} \int_{0}^{\infty} e^{-u}\ du \\ &=\frac{1}{\pi ({y_1}^2 + 1)}\ \ \end{align}$$임을 알 수 있다.
6-1. 위에서 구한 $Y_1$의 분포를 모수가 $0$, $1$인 코시분포 또는 표준코시분포(standard Cauchy distribution)라고 하며 $\text{Cauchy}(0, 1)$로 표기한다. 즉, 서로 독립인 표준정규확률변수의 비는 표준코시분포를 따른다. 코시분포의 가장 큰 특징은 평균을 비롯한 적률을 가지지 않는다는 것이다.

7. 확률변수 $X_1$, $X_2$가 서로 독립일 때 그 합인 $Y_1 = X_1 + X_2$의 확률밀도함수를 구해 보자. $Y_2 = X_2$로 두면 $X_1 = Y_1 - Y_2$, $X_2 = Y_2$이고 $\vert \det \mathbf{J}_{\mathbf{u}^{-1}} \vert = 1$이다. 따라서 $$ \begin{align} f_{Y_1} (y_1) &= \int_{-\infty}^{\infty }f_{Y_1, Y_2}(y_1, y_2)\ dy_2 \\ &= \int_{-\infty}^{\infty} f_{X_1}(y_1 - y_2) f_{X_2}(y_2)\ dy_2 \\ &= \int_{-\infty}^{\infty} f_{X_1}(y_1 - \tau) f_{X_2} (\tau)\ d\tau \end{align} $$의 합성곱(convolution) 형태를 얻는다. 예를 들어 서로 독립인 표준정규확률변수의 합의 분포는 확률밀도함수 $$\begin{align} f(x) &= \int_{-\infty}^{\infty} \phi(x-\tau) \phi(\tau)\ d\tau \\ &= \frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{-\frac{(x-\tau)^2 + \tau^2}{2}}\ d \tau \\ &=\frac{1}{2 \pi}e^{-\frac{x^2}{4}}\int_{-\infty}^{\infty}e^{-\left(\tau-\frac{x}{2} \right)^2}\ d \tau \\ &=\frac{1}{2 \sqrt{\pi}} e^{-\frac{x^2}{4}} \end{align}$$로 표현되며, 이는 $\text{N}(0, 2)$에 해당한다.
References
김우철, 개정판 수리통계학
송성주·전명식, 수리통계학 제5판
'일반통계학' 카테고리의 다른 글
| [일반통계학] 13. 확률변수의 수렴 (0) | 2022.01.28 |
|---|---|
| [일반통계학] 12. 표본분포 (0) | 2022.01.09 |
| [일반통계학] 10. 야코비안 (0) | 2021.12.05 |
| [일반통계학] 9. R을 이용한 분포의 계산 (0) | 2021.12.03 |
| [일반통계학] 8. 정규분포 (0) | 2021.11.20 |


